Chemical Equation Balancer - In your terminal

Screenshot 2024-09-17 055339

This terminal-based C++ chemical equation balancer parses equations into vectors and balances them using row operations, supporting equations with ions and water of crystallization

I had been planning to write about this project for long but just delayed it until now (about 6 months of procastination). Though fairly simple project, the math and few concepts I learned while implementing this project is something worth while to talk about, I think.

First of all the basic overview of this project:

Github Link

Overview of Program

You input equation in your standard form and get the balanced equation as output. It also supports water of crystallization, electrons and ions in the equation.

Standard Chemical Equations:

The program balances typical chemical reactions of the form [Reactants] -> [Products].
Example:
```
Input: H2 + O2 -> H2O  
Output: (2) H2 + (1) O2 -> (2) H2O
```
Water of Crystallization:

The program can handle chemical equations involving water of crystallization, represented as .H2O in the reactants or products.
Example:
```
Input: CuSO4.5H2O -> CuSO4 + H2O  
Output: (1) CuSO4.5H2O -> (1) CuSO4 + (5) H2O
```
Ionic Equations:

The program supports balancing equations that involve ions, where ions are denoted inside { }.
Example:
```
Input: Fe{+3} + I{-1} -> Fe{+2} + I2  
Output: (2) Fe{+3} + (2) I{-1} -> (2) Fe{+2} + (1) I2
```
Electron (e⁻) in equation

Equations involving electrons can also be balanced.
Example:
```
Input: O2 + H{+1} + e -> H2O  
Output: (1) O2 + (4) H{+1} + (4) e -> (2) H2O
```

And this is a example of how it can solve typical problems: Screenshot 2024-09-17 055203

Understanding the Program

Now lets talk about the workflow of this application. There is just two part of the program:

Take string input from user and parse it into coefficient matrix
Say user gives: H2 + O2 -> H2O as input. Then the first step is to convert each term into column matrix.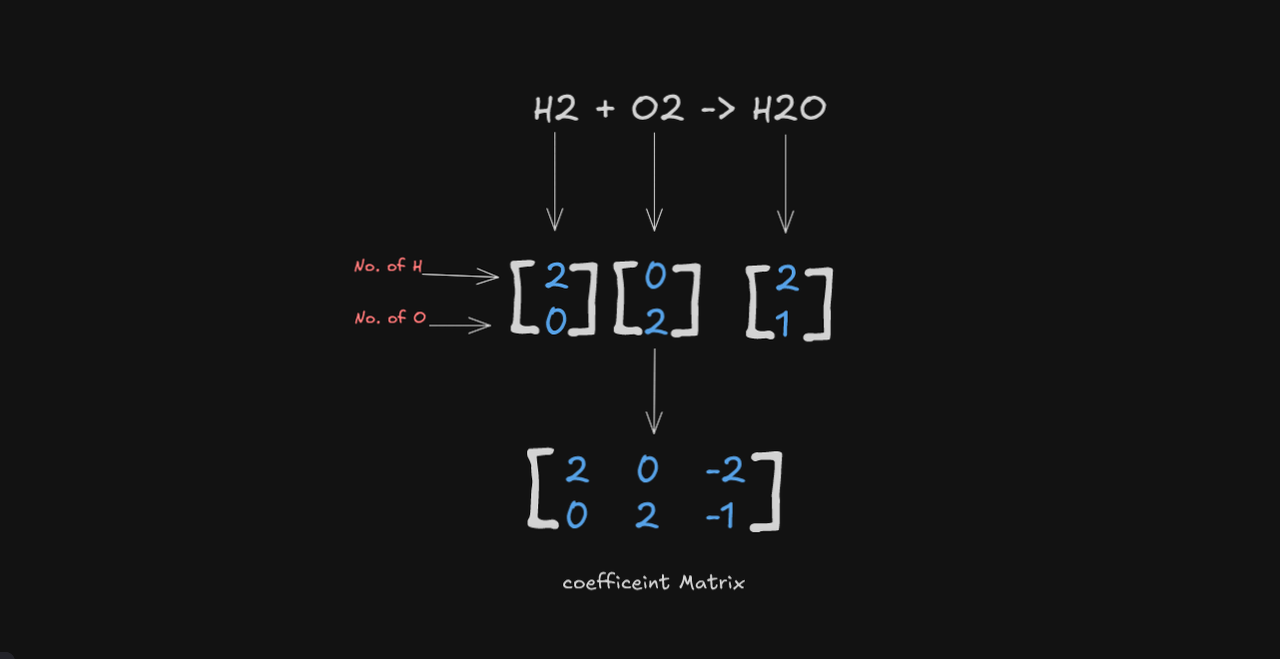
Next step is to convert this into Echleon Matrix form.
Here the final column will help to provide our required coefficients. But first we need to make it all integers.

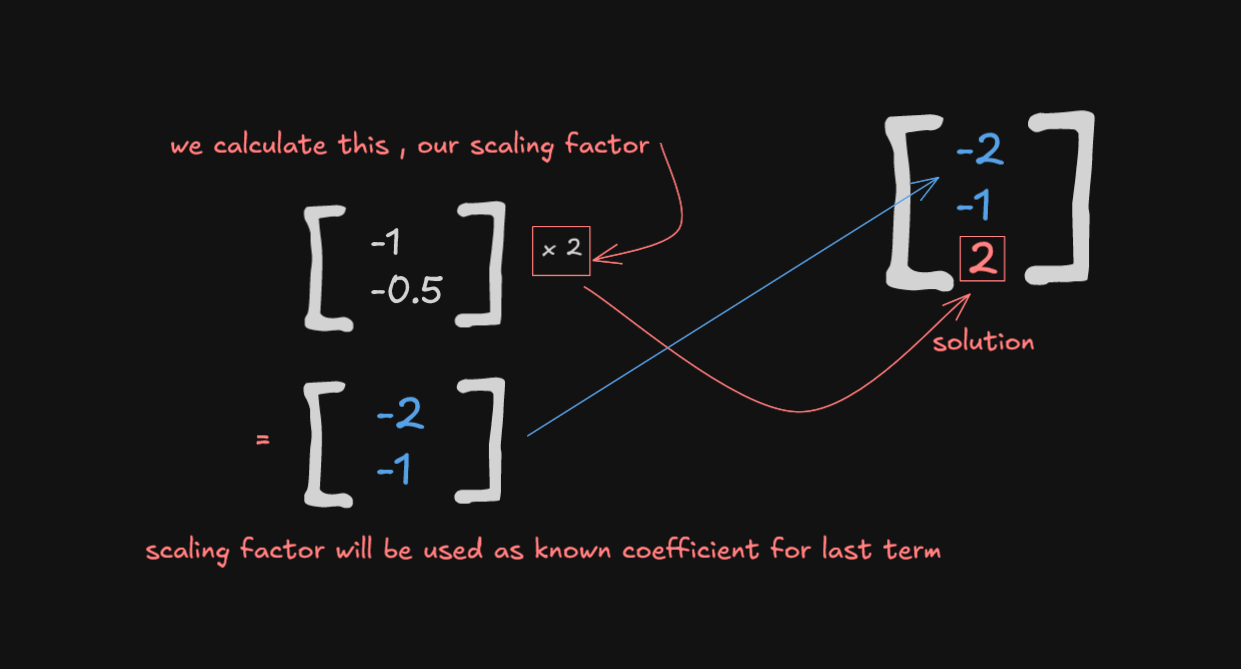
Getting Coefficient of H2O

This vector we obtained will help use get our final answer, but some fine tuning remaining. To make sure that we get the smallest integer set, we divide by greatest common divisor of the numbers and also multiply by (-1). This will make sure that reactant side will have (+ve) integers while product side will have (-ve) integers.

Final Steps

And now we have final answer

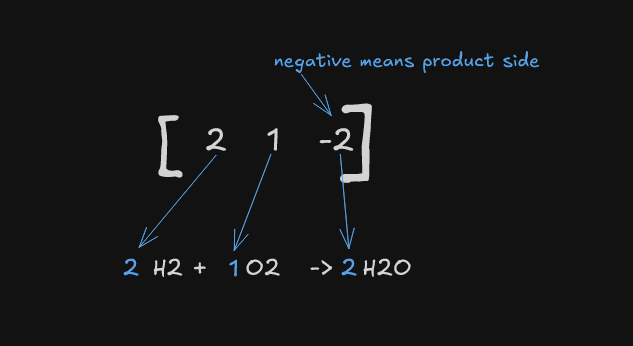
And thats how it works. We can extend this for water of crystallization, ionization and charges. Some modification in matrix. But the main idea remains the same.

Why ? Because, thrill of a challenge

Motivation for doing this small program is the thrill of uncertainty whether i can actually make it. I know the concept, I have learnt it in college but can i actually implement it. It is sometime fun to do these kinds of small and sweet mathematical programming.